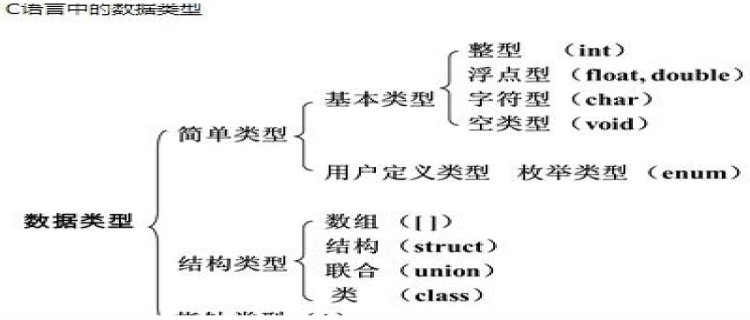
独立同分布变量是指在概率统计理论中,随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布。
在概率统计理论中,随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布,这些变量称为独立同分布变量。

独立同分布最早应用于统计学,随着科学的发展,独立同分布已经应用数据挖掘,信号处理等不同的领域。
定义
在概率统计理论中,随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布的,这些变量称为独立同分布变量。
性质:
(1)服从同一分布
(2)相互独立
随机变量
以一维随机变量为例:
观察一个随机现象,其样本点可以是具有数量性质的,也可能是非数量性质的,前者如抛一枚骰子,可能出现的点数是 1 点、2 点、…、6 点;后者如掷一枚硬币,可能出现正面,也可能出现反面,约定:“出现正面”记为 1,“出现反面”记为 0。无论是哪一种情形,都体现出这样的共同点:对随机试验的每一个可能结果,有唯一一个实数与之对应。这种对应关系实际上定义了样本空间
设
相互独立
在概率论中,相互独立,是设
注:若
推广:
设
更一般的定义是,
概率分布
(1)均匀分布
设连续型随机变量 X 具有概率密度
(2)指数分布
设连续型随机变量 X 具有概率密度
其中,
(3)正态分布
设连续型随机变量 X 的概率密度为:
例题
已知随机变量
解答:
设