正态分布
若X的概率密度函数为:
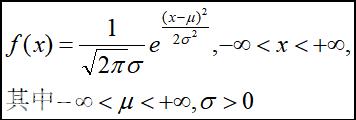
正态分布
特征:
f(x)关于x=μ对称x=μ的左侧是单调递增函数,右侧是单调递减函数x=μ时,f(x)取得最大值1/(σ*(2π)^(1/2))|x-μ|→∞是f(x)→0μ、σ的意义
当σ固定不变时,改变μ的大小,f(x)图形的形状不变,只是沿着x轴平移图形。因此μ称为位置参数(决定对称轴位置)。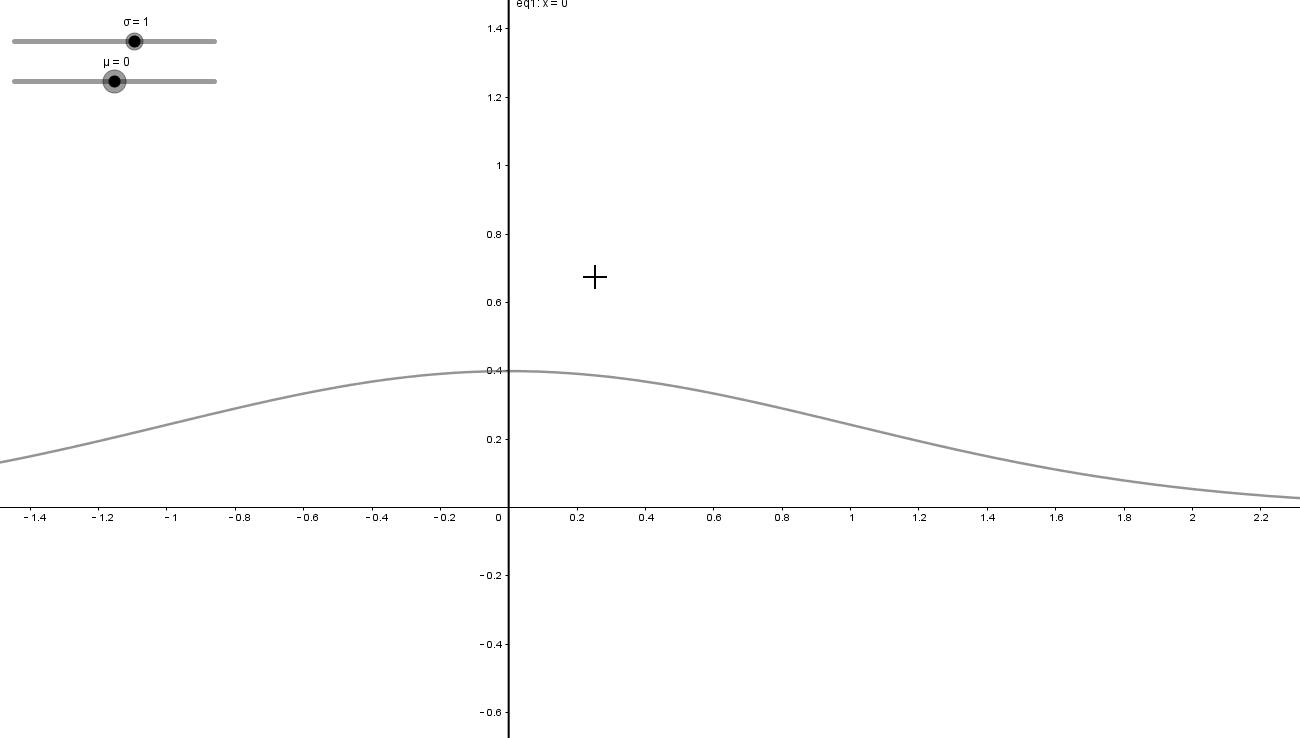
尺度参数σ
现实中的正态分布
人的生理特征满足正态分布医学检测指标满足正态分布可以使用正态分布近似多个随机变量的和正态分布概率的计算
若X~N(μ,σ^2),则:
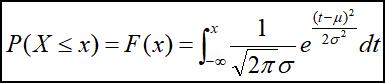
标准正态分布概率密度函数
记为φ(z),其对应的分布函数
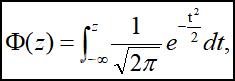
标准正态分布函数表
非标准正态分布函数计算
前面提到非标准正态分布也可以查表,我们第一步需要将非标准正态分布转换为标准正态分布:
对X~N(μ,σ^2)时:
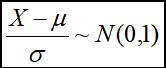
计算非标准正态分布函数
我们可以很方便地查表得到计算值。
实验:探究多个随机数的和频次分布情况
设计一个python实验,验证10个随机整数和符合正态分布图形。代码如下:
import matplotlib.pyplot as pltimport randomsums = {}for i in range(100000): sum = 0 for j in range(10): sum += random.randint(1, 10) sums[sum] = sums.get(sum, 0) + 1x = list(sums.keys())y = list(sums.values())fig = plt.figure() # 创建画图窗口ax1 = fig.add_subplot(1, 1, 1) # 将窗口划分为2行一列,选择第一块区域画图ax1.set_xlabel('x') # 设置x轴标签ax1.set_ylabel('y') # 设置y轴标签ax1.scatter(x, y)
10个随机数的和频次分布图
我们清晰的可以从图中到随机数之和频次分布满足正态分布图形。












