邻接矩阵(adjacency matrix)是一种方阵,用来表示有限图。它的每个元素代表各点之间是否有边相连。图的关联矩阵需要和邻接矩阵区分。
在图论和计算机科学中,邻接矩阵(adjacency matrix)是一种方阵,用来表示有限图。它的每个元素代表各点之间是否有边相连。
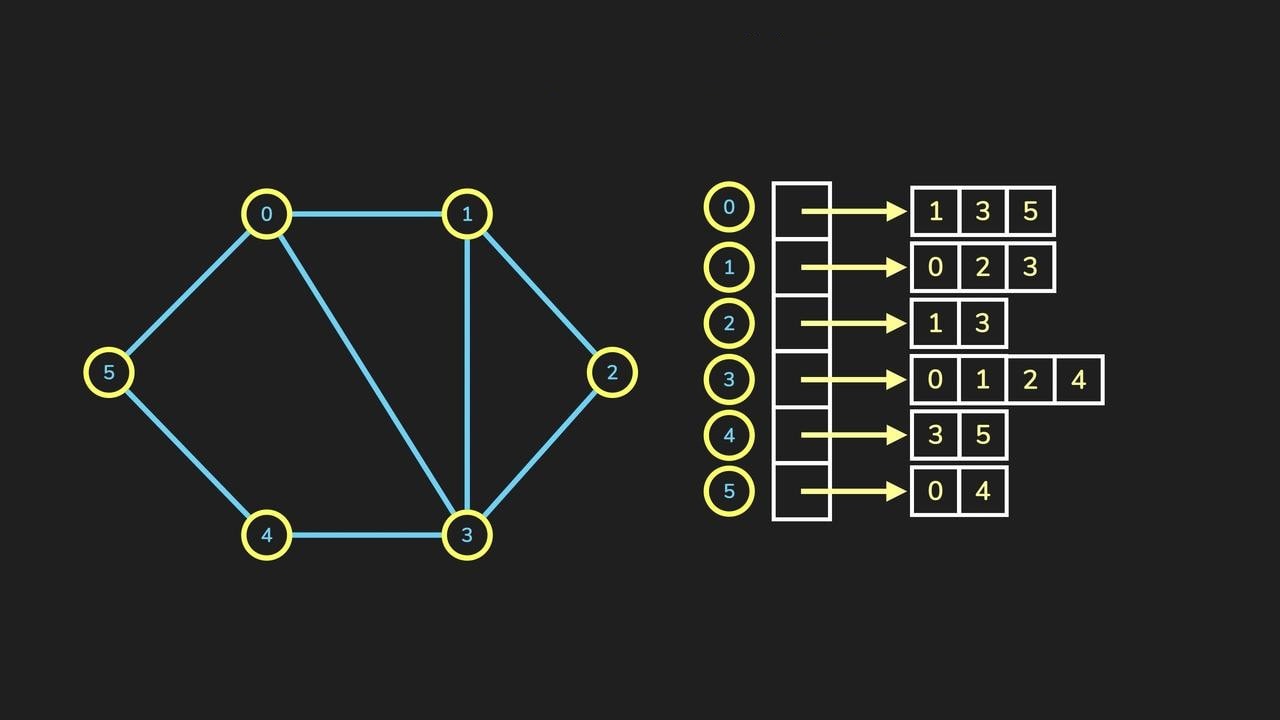
作为特例,简单图的邻接矩阵是(0,1)矩阵并且对角线元素都为 0。无向图的邻接矩阵是对称矩阵。图和其邻接矩阵的特征值和特征向量之间的关系是谱图理论的研究对象。
图的关联矩阵需要和邻接矩阵区分。它是图的另一种矩阵表示方式,它的元素表示各个节点-边对是否相关。还有图的度数矩阵,含有每个结点的度数信息。
逻辑结构分为两部分:V 和 E 集合,其中,V 是顶点,E 是边。因此,用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。
定义
邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。设 G=(V,E)是一个图,其中 V={v1,v2,…,vn}。G 的邻接矩阵是一个具有下列性质的 n 阶方阵:
1.对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为 0,有向图则不一定如此。
2.在无向图中,任一顶点 i 的度为第 i 列(或第 i 行)所有非零元素的个数,在有向图中顶点 i 的出度为第 i 行所有非零元素的个数,而入度为第 i 列所有非零元素的个数。
3.用邻接矩阵法表示图共需要 n^2 个空间,由于无向图的邻接矩阵一定具有对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要 n(n-1)/2 个空间。
特点
无向图的邻接矩阵一定是对称的,而有向图的邻接矩阵不一定对称。因此,用邻接矩阵来表示一个具有 n 个顶点的有向图时需要 n^2 个单元来存储邻接矩阵;对有 n 个顶点的无向图则只存入上(下)三角阵中剔除了左上右下对角线上的 0 元素后剩余的元素,故只需 1+2+…+(n-1)=n(n-1)/2 个单元。
无向图邻接矩阵的第 i 行(或第 i 列)非零元素的个数正好是第 i 个顶点的度。
有向图邻接矩阵中第 i 行非零元素的个数为第 i 个顶点的出度,第 i 列非零元素的个数为第 i 个顶点的入度,第 i 个顶点的度为第 i 行与第 i 列非零元素个数之和。
用邻接矩阵表示图,很容易确定图中任意两个顶点是否有边相连。














