摘要:在数学中,我们常常将平面直角坐标系分成四个象限,分别是第一象限、第二象限、第三象限和第四象限。其中,第一象限是指$x0$,$y0$的区域第二象限是指$x00$的区域第三象限是指$x00$,$y<0$的区域。
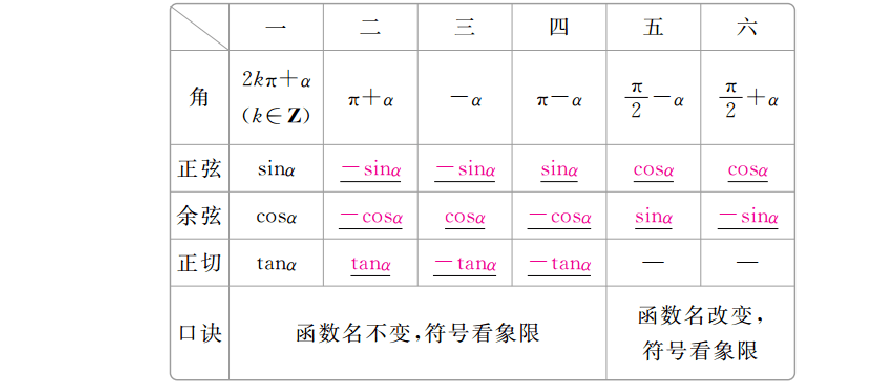
奇变偶不变符号是数学中一个重要的概念,它在数学的各个分支中都有广泛的应用。在数学中,我们经常需要研究函数的性质,其中一个重要的性质就是函数的奇偶性。而奇变偶不变符号就是用来描述函数奇偶性的一种方法。
在数学中,我们常常将平面直角坐标系分成四个象限,分别是第一象限、第二象限、第三象限和第四象限。其中,第一象限是指$x>0$,$y>0$的区域;第二象限是指$x0$的区域;第三象限是指$x<0$,$y0$,$y<0$的区域。
当我们研究一个函数的时候,我们可以通过观察它在各个象限中的表现来判断它的奇偶性。如果一个函数在第一象限和第三象限中的取值相等,在第二象限和第四象限中的取值也相等,那么我们就称这个函数是偶函数,用$E$来表示。如果一个函数在第一象限和第三象限中的取值相等,但在第二象限和第四象限中的取值相反,那么我们就称这个函数是奇函数,用$O$来表示。
为了方便描述函数的奇偶性,我们引入了奇变偶不变符号。对于一个函数$f(x)$,我们定义它的奇变偶不变符号为:
$$
begin{cases}
+1, & f(-x)=f(x) \
-1, & f(-x)=-f(x)
end{cases}
$$
当$f(x)$是偶函数时,它的奇变偶不变符号为$+1$;当$f(x)$是奇函数时,它的奇变偶不变符号为$-1$。可以看出,奇变偶不变符号只和函数在$x=0$处的取值有关,因此我们也可以将它定义为:
$$
begin{cases}
+1, & f(0)=f(-0) \
-1, & f(0)=-f(-0)
end{cases}
$$
奇变偶不变符号在数学中有广泛的应用。比如,在微积分中,我们经常需要求函数的不定积分和定积分,而函数的奇偶性可以帮助我们简化积分的计算。比如,对于一个偶函数$f(x)$,它的定积分可以化为:
$$
int_{-a}^a f(x)dx=2int_0^a f(x)dx
$$
这个公式的证明就是利用了偶函数的性质。同样地,对于一个奇函数$f(x)$,它的定积分可以化为:
$$
int_{-a}^a f(x)dx=0
$$
这个公式的证明也是利用了奇函数的性质。
除了在微积分中,奇变偶不变符号还在其他数学分支中有广泛应用。比如,在代数学中,我们可以通过奇变偶不变符号来判断一个多项式是否为奇函数或偶函数。在群论中,我们可以通过奇变偶不变符号来研究群的性质。在拓扑学中,奇变偶不变符号也有很重要的应用。
总之,奇变偶不变符号是数学中一个非常重要的概念,它可以帮助我们简化计算,研究函数的性质,以及在各个数学分支中应用。











